Quiz 3.10:
Question:
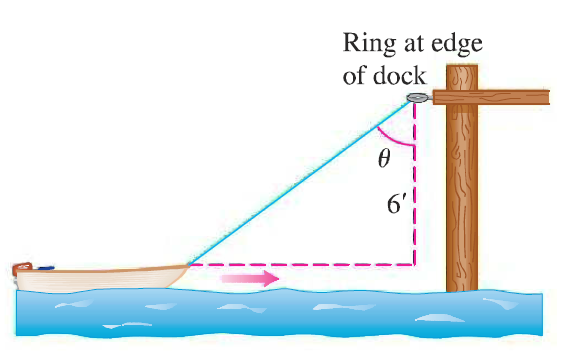
A dinghy is pulled toward a dock by a rope from the bow through a ring on the dock 6 ft. above the bow. The rope is being hauled in at a rate of 2 ft/sec. How fast is the boat approaching the dock when 10 ft of rope are out?

Solution:
Let \( a \) be the distance from the dock and \( c \) be the amount of rope out. Both measured in feet.
By the Pythagorean Theorem, we have \( a^2+36=c^2 \)
Differentiating that equation implicitly with respect to \( t \) gives \( 2a \frac{da}{dt}=2c \frac{dc}{dt} \)
We were given that \( \frac{dc}{dt}=-2 \) ft/s
We were asked for \( \frac{da}{dt} \) when \( c=10 \), which by Pythagoras would mean \( a=8 \)
So putting that all together get get,
\( 2(8)\frac{da}{dt}=2(10)(-2) \)
\( \frac{da}{dt}=\frac{-10}{4}=-\frac{5}{2} \) ft/s
By the Pythagorean Theorem, we have \( a^2+36=c^2 \)
Differentiating that equation implicitly with respect to \( t \) gives \( 2a \frac{da}{dt}=2c \frac{dc}{dt} \)
We were given that \( \frac{dc}{dt}=-2 \) ft/s
We were asked for \( \frac{da}{dt} \) when \( c=10 \), which by Pythagoras would mean \( a=8 \)
So putting that all together get get,
\( 2(8)\frac{da}{dt}=2(10)(-2) \)
\( \frac{da}{dt}=\frac{-10}{4}=-\frac{5}{2} \) ft/s
