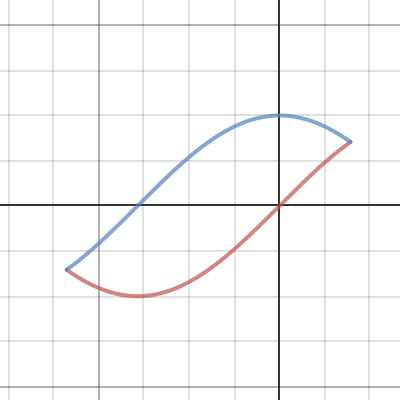
Quiz 5.6:
Question:
Find the area of one of the regions enclosed by \( \sin x \) and \( \cos x \)
Solution:
There are infinitely many regions, but they are all congruent.
We need to first find two consecutive points of intersection, so we can get our limits of integration.
\( \sin x = \cos x \)
\( \tan x = 1 \)
\( x= -\frac{3\pi}{4} , \frac{\pi}{4} \)
On this interval \( \cos x \) is the larger function, so we have,
\( \int \limits _{-\frac{3\pi}{4}} ^{\frac{\pi}{4}} \left ( \cos x - \sin x \right ) dx \)
\( = \left [ \sin x + \cos x \right ] _{-\frac{3\pi}{4}} ^ {\frac{\pi}{4}} \)
\( = \left ( \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2} \right ) - \left (- \frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2} \right ) \)
\( = 2\sqrt{2} \)
We need to first find two consecutive points of intersection, so we can get our limits of integration.
\( \sin x = \cos x \)
\( \tan x = 1 \)
\( x= -\frac{3\pi}{4} , \frac{\pi}{4} \)
On this interval \( \cos x \) is the larger function, so we have,
\( \int \limits _{-\frac{3\pi}{4}} ^{\frac{\pi}{4}} \left ( \cos x - \sin x \right ) dx \)
\( = \left [ \sin x + \cos x \right ] _{-\frac{3\pi}{4}} ^ {\frac{\pi}{4}} \)
\( = \left ( \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2} \right ) - \left (- \frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2} \right ) \)
\( = 2\sqrt{2} \)