Quiz 8.2:
Question:
To measure the Eiffel Tower in Paris, a person stands away from the base and measures the angle of elevation to the top of the tower to be \( 60 ^\circ \). Moving 210 ft. closer, the angle of elevation to the top is \( 70 ^\circ \). How tall is the Eiffel Tower?
5th Ed: #35
5th Ed: #35
Solution:
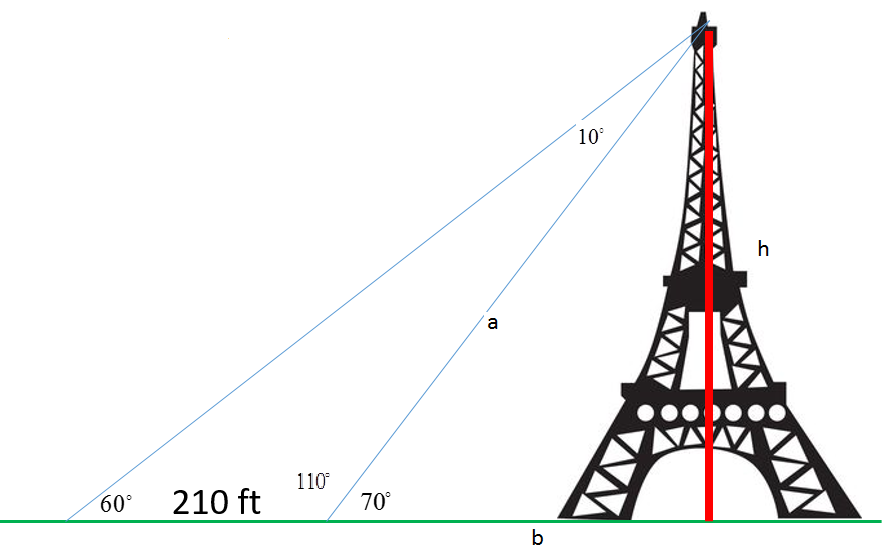
Using Law of Sines on the outer triangle
\( \frac{\sin 60^\circ}{a}=\frac{\sin 10^\circ}{210} \)
\( a= \frac{210\sin 60^\circ}{\sin 10^\circ} \)
Using right triangle trigonometry on the inner right triangle
\( \sin 70^\circ = \frac{h}{a} \)
\( h = a \sin 70^\circ \)
Combining the two
\( h=\frac{210 \left ( \sin 60^\circ \right ) \left ( \sin 70^\circ \right ) }{\sin 10^\circ} \)
Solution (Alternate):
Using Law of Sines on the outer triangle
\( \frac{\sin 60^\circ}{a}=\frac{\sin 10^\circ}{210} \)
\( a= \frac{210\sin 60^\circ}{\sin 10^\circ} \)
Using right triangle trigonometry on the inner right triangle
\( \sin 70^\circ = \frac{h}{a} \)
\( h = a \sin 70^\circ \)
Combining the two
\( h=\frac{210 \left ( \sin 60^\circ \right ) \left ( \sin 70^\circ \right ) }{\sin 10^\circ} \)
Solution (Alternate):
\( \tan 70 ^\circ=\frac{h}{b} \) therefore \( b = \frac{h}{\tan 70 ^\circ} \)
\( \tan 60 ^\circ=\frac{h}{210+b} \) therefore \( b = \frac{h}{\tan 60 ^\circ}-210 \)
Equating the \(b\), we get
\( \frac{h}{\tan 70^\circ} = \frac{h}{\tan ^\circ 60} - 210 \)
\( h = \frac{-210}{\frac{1}{\tan 70^\circ}-\frac{1}{\tan 60^\circ}} \)
\( \tan 60 ^\circ=\frac{h}{210+b} \) therefore \( b = \frac{h}{\tan 60 ^\circ}-210 \)
Equating the \(b\), we get
\( \frac{h}{\tan 70^\circ} = \frac{h}{\tan ^\circ 60} - 210 \)
\( h = \frac{-210}{\frac{1}{\tan 70^\circ}-\frac{1}{\tan 60^\circ}} \)
